La Saint Amour, c'est le 9 août

Je cède à la pression : c'est la fête des amoureux, je suis amoureuse, je suis concernée.

Par contre, je suis calmée par l'ampleur du phénomène, l'amour en plastique vendu dans toutes les boutiques. Les peluches c'est bien mignon mais ça prend la poussière, le chocolat j'en mange toute l'année, je n'attends ni noël, pâques ou la St V. pour remonter mon taux de magnésium (j'aime essayer d'être heureuse tout le temps, c'est pour ça), des bisous et des câlins j'en ai tous les jours (s'ils ne viennent pas à moi, je sais où les trouver).

Bref, comme toutes les célébrations synchronisées, on aimerait que la démarche soit distillée dans les 365 jours de l'année.

La phrase "c'est pas tous les jours la fête" m'amuse, parce que, oui, certains jours sont spéciaux et on les vit intensément; mais le "mieux" n'est possible que s'il succède au moins bien et ce passage se fait pour des raisons plus concrètes qu'un changement de date.

J'ai donc bien envie de vous parler d'amour aujourd'hui, mais par un biais moins marchandisé.

La première photo est celle qui a illustré l’exposition de Yann Arthus-Bertrand "La terre vue du ciel", elle représente le Coeur de Voh en Nouvelle-Calédonie (dédicace aux amoureux de l'autre côté de la terre : Hervé et johana).

Le nuage en coeur est dédicacé aux coeurs romantiques qui savent voir la beauté incontrôlée, même pas voulue, de tout ce qui nous entoure. "La beauté est dans l'oeil de celui qui regarde" (réflexion ultra philosophique : quelles sont les qualités qui appartiennent à l'objet, quel part de subjectivité dans nos perceptions? Réponse : énorme contribution du sujet dans sa vision du monde et des autres).

Ensuite, ces mains qui tendent du riz me rappellent les missions humanitaires, contribution du bout des doigts de l'occident aisé vers les pays en voie de développement. Ces mains me rappellent aussi que l'amour ce n'est pas que le couple, et je suis pressée que ma famille s'agrandisse (observez bien : il y a une main adulte sous celles de l'enfant; ce ne serait pas ça le symbole du rôle de parent : parer à la chute éventuelle).

Pour les fleurs, si j'ai évité les écueils du cadeau classique de l'homme qui aime (ou trompe) sa femme, j'aime les jeux de mots, et là ce sont des "coeurs de fleurs". Pour continuer dans la thématique jeux de mots : des emporte-coeurs en forme de coeur; autant ça craint comme cadeau (l'homme qui réduit sa femme à une fée du logis), autant si on les possède déjà, c'est le bon jour pour les utiliser. Faites des petits gâteaux en forme de coeur si ça vous éclate, c'est pas ça être piégé par le système. Fabriquez votre petite carte perso à l'élu de votre coeur, même si môssieu a spécifié que la St V. ne passerait pas par lui; expliquez-lui que c'est contagieux mais qu'on peut s'en sortir avec des petites attentions.

La mienne, d'attention pour mon chéri, ce sera ce message que lui seul pourra résoudre (ou alors contredisez-moi dans les commentaires) :

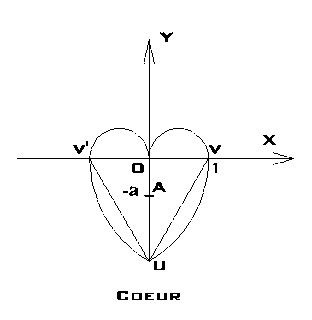
On considère une figure géométrique en forme de coeur constituée de quatre arcs de cercle, construite comme décrit ci-après.
On part d'un triangle équilatéral et on construit deux demi-cercles de mêmes dimensions tangents entre eux, comme indiqué sur la figure ci-dessus.

On construit ensuite deux arcs de cercle centrés sur deux sommets du triangle équilatéral, de rayons égaux au côté du triangle ( voir figure ).
Objet du problème :
On cherche à déterminer le cercle de rayon minimal englobant cette figure, centre et rayon.
On admet qu'un tel cercle existe, est unique, et que, compte tenu de la symétrie de la figure, son centre est justement situé sur l'axe de symétrie de cette figure.
Méthode employée :
Nous allons utiliser la géométrie analytique pour déterminer ce cercle.
Pour ce faire, nous rapportons le plan à un repère orthonormé direct OXY, tel que (OY) soit axe de symétrie de la figure et que chacun des demi cercles ait pour diamètre 1.
A, d'abscisse -a, est un point variable de l'axe (OY) pour lequel nous allons chercher le rayon minimal d'un cercle centré sur lui et englobant la figure.
Nous rechercherons ensuite la valeur minimale de ce rayon minimal lorsque A varie sur l'axe (OY) ainsi que la position correspondante de A, appelé Ao ( pour A optimal ).
Au travail :
Montrez d'abord par un argument géométrique simple faisant intervenir le point V, que le point Ao est nécessairement situé sous l'axe des abscisses.
Montrez de même que Ao est situé au dessus du point U.
Calculez, en fonction de a, le rayon r minimal que doit posséder un cercle de centre A pour qu'il englobe l'un quelconque des deux demi-cercles du coeur.
Dites quelle est alors la position relative du cercle correspondant avec chacun des deux demi-cercles.
Déterminez pour quelle position A' de A, A' d'abscisse -a', A est équidistant de U et V. Déterminez a'.
Pour A appartenant au segment [UA'], on considère un point M variable sur l'arc de cercle (UV) ( orienté de U vers V ). Sachant que l'angle (V'U,V'A) est inférieur à Pi/6 ( à justifier ) et appelant m l'angle (V'U,V'M), montrez que A est toujours plus proche de M que de V ( pensez médiatrice ).
Déterminez la valeur correspondante r1 du rayon minimal d'un cercle centré sur A englobant les deux derniers arcs de cercles du coeur.
Même question lorsque A appartient au segment [A'O]. Déterminez r2 ...
Pour A appartenant à [UA'], la valeur minimale du rayon d'un cercle centré sur A et englobant le coeur tout entier est donc la valeur minimale du maximum de r et r1 sur cette plage de valeurs.
Déterminez cette valeur minimale qu'on appellera R1 et l'abscisse de la position de A pour laquelle elle est atteinte ( constatez que c'est -a' ).
Indication : vous commencerez par comparer r et r1, bien sûr !
Pour A appartenant à [A'O], la valeur minimale du rayon d'un cercle centré sur A et englobant le coeur tout entier est cette fois la valeur minimale du maximum de r et r2 sur cette autre plage de valeurs.
Déterminez cette valeur minimale qu'on appellera R2 et l'abscisse de la position de A pour laquelle elle est atteinte ( constatez que c'est une valeur particulière non encore rencontrée pour le moment : vous l'appellerez -a" ).
Comparez R1 et R2 et déterminez ainsi -ao ( abscisse de Ao ) et la valeur Rmin du rayon minimal de tous les cercles englobant le coeur.
Tracez les représentations graphiques de r, r1 et r2 et retrouvez graphiquement les résultats précédents.
Pour les élèves rapides : Calculez une valeur approchée à trois chiffres derrière la virgule du rapport des aires du coeur et du cercle minimal.

Wow, il va s'éclater! Vous moins, je pense (si vous êtes comme moi)...

Et pour vous, les petites attentions de la st V. ou de tous les jours, ce serait quoi par exemple?